minhui study
05. 훈련노하우 - 규제 방법과 교차 검증 본문
05-3 규제 방법을 배우고 단일층 신경망에 적용하기
왼쪽의 그래프를 보았을 때 검정색과 파란색 선 둘 중에 어떤 선이 점들을 더 잘 표현한 것일까?
보통 이런 경우 경사가 급한 그래프보다는 경사가 완만한 그래프가 성능이 더 좋다고 평가한다.
오른쪽 그래프는 몇 개의 데이터에 집착한 나머지 박스로 표시한 샘플 데이터를 제대로 표현하지 못한 경우를 보여주고 있다. 이런 경우를 '모델이 일반화되지 않았다'라고 말한다.

이럴 때 규제를 사용하여 가중치를 제한하면 모델이 몇 개의 데이터에 집착하지 않게 되어 일반화 성능을 높일 수 있다.
대표적인 규제 기법은 L1규제와 L2규제를 살펴보고 규제를 적용했을 때 손실함수의 그래프가 어떻게 변하는지도 알아보자
L1 규제
'가중치의 절댓값을 손실 함수에 더한 것'
- 손실 함수에 L1 노름을 더하면 L1 규제 만들어진다. 이 때 L1 노름을 그냥 더하지 않고 규제의 양을 조절하는 파라미터 a(알파)를 곱한 후 더한다.
* L1노름(norm) : 가중치의 절댓값
* L1노름의 n : 가중치의 개수 - 알파는 L1 규제의 양을 조절하는 하이퍼파라미터이다.
- 알파 값이 크면 전체 손실함수 값이 커지지 않도록 w값의 합이 작아져야 한다. ▷ 규제가 강해진다.
- 알파 값이 작으면 w의 합이 커져도 손실 함수 값이 큰 폭으로 커지지 않는다 ▷ 규제가 약해진다.
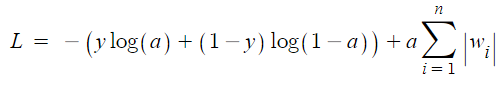
L1 규제의 미분
- 절대값 |w|를 w에 대해 미분하면 w 값의 부호만 남기 때문에 w의 부호라는 의미로 sign(w)라고 표현한다.
- L1 규제를 적용한 손실 함수의 도함수에 학습률을 곱하면 학습률을 적용시킬 수 있다.
- 규제 하이퍼파라미터 alpha와 가중치의 부호를 곱해서 업데이트할 그레디언트에 더해 주면 된다.
→ w_grad = w_grad + alpha * np.sign(w)
* alpha 변수가 규제 하이퍼파라미터이다.
* np.sign() 함수는 배열 요소의 부호를 반환한다. - 위의 식에서는 절편에 대해 규제를 하지 않는다. (복잡도에는 영향을 주지 않기 때문이다.)
- SGDClassfier 클래스에서는 penalty 매개변수 값을 L1으로 지정하는 방법으로 L1 규제를 적용할 수 있다.
+ 라쏘(Lasso) 모델
회귀 모델에 L1 규제를 추가한 것
- 일부 가중치를 0으로 만들 수 있다. ( 가중치가 0인 특성은 모델에서 사용할 수 없다는 것과 같은 의미이므로 특성을 선택하는 효과를 얻을 수 있다. )
- L1 규제는 규제 하이처차라미터 알파에 많이 의존한다. 즉, L1은 가중치 크기에 따라 규제의 양이 변하지 않으므로 규제 효과가 좋다고 말할 수 없다.
L2 규제
'가중치에 대한 L2 노름의 제곱을 손실 함수에 더한 것'
L1 규제와 마찬가지로 규제의 양을 조절하기 위한 하이퍼파라미터이고 1/2은 미분 결과를 좋게 하기 위하여 추가한 것이다.

L2 규제의 미분
- L2 규제를 미분하면 간단히 가중치 벡터 w만 남는다.
- L2 규제를 경사 하강법 알고리즘에 적용하기 위해서는 그레디엍느에 alpha와 가중치의 곱을 더하면 된다.
w_grad += alpha * w - L2 규제는 그레이디언트 계산에 가중치의 값 자체가 포함되므로 가중치의 부호만 사용하는 L1 규제보다 조금 더 효과적이다.
- L2 규제는 가중치를 완전히 0으로 만들지 않는다. 가중치를 완전히 0으로 만들면 특성을 제외하는 효과는 있지만 모델의 복잡도가 떨어지므로 L2 규제를 널리 사용한다.
+ 릿지(Ridge) 모델
'회귀 모델에 L2 규제를 적용한 것'
- SGDClassfier 클래스에서는 penalty 매개변수 L2로 지정하여 L2 규제를 추가할 수 있다.
- 사이킷런에서는 릿지 모델을 sklearn.linear_model.Ridge 클래스로 제공한다.
| L1 규제 | L2 규제 |
| 그레이디언트에서 alpha에 가중치의 부호를 곱하여 그레이디언트에 더한다. | 그레이디언트에서 alpha에 가중치를 곱하여 그레이디언트에 더한다. |
| w_grad = w_grad + alpha * np.sign(w) | w_grad += alpha * w |
로지스틱 회귀에 규제 적용하기
1. 그레이디언트 업데이트 수식에 페널티 항 반영하기
먼저 __init()__ 메서드에 L1 규제와 L2 규제의 강도를 조절하는 매개변수 l1와 l2를 추가한다. 기본값은 0이다.
(이때 규제 적용 안함)
class SingleLayer:
def __init__(self, learning_rate=0.1, l1=0, l2=0):
self.w = None
self.b = None
self.losses = []
self.val_losses = []
self.w_history = []
self.lr = learning_rate
self.l1 = l1
self.l2 = l2
2. fit() 메서드에서 역방향 계산을 수행할 때 그레이디언트에 페널티 항의 미분값을 더한다.
L1 규제와 L2 규제를 따로 적용하지 않고 하나의 식으로 작성하여 두 규제를 동시에 수행할 수 있다.
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
self.w = np.ones(x.shape[1]) # 가중치를 초기화합니다.
self.b = 0 # 절편을 초기화합니다.
self.w_history.append(self.w.copy()) # 가중치를 기록합니다.
np.random.seed(42) # 랜덤 시드를 지정합니다.
for i in range(epochs): # epochs만큼 반복합니다.
loss = 0
# 인덱스를 섞습니다
indexes = np.random.permutation(np.arange(len(x)))
for i in indexes: # 모든 샘플에 대해 반복합니다
z = self.forpass(x[i]) # 정방향 계산
a = self.activation(z) # 활성화 함수 적용
err = -(y[i] - a) # 오차 계산
w_grad, b_grad = self.backprop(x[i], err) # 역방향 계산
# 그래디언트에서 페널티 항의 미분 값을 더합니다
w_grad += self.l1 * np.sign(self.w) + self.l2 * self.w
self.w -= self.lr * w_grad # 가중치 업데이트
self.b -= b_grad # 절편 업데이트
# 가중치를 기록합니다.
self.w_history.append(self.w.copy())
# 안전한 로그 계산을 위해 클리핑한 후 손실을 누적합니다
a = np.clip(a, 1e-10, 1-1e-10)
loss += -(y[i]*np.log(a)+(1-y[i])*np.log(1-a))
# 에포크마다 평균 손실을 저장합니다
self.losses.append(loss/len(y) + self.reg_loss())
# 검증 세트에 대한 손실을 계산합니다
self.update_val_loss(x_val, y_val)
3. 로지스틱 손실 함수 계산에 페널티 항 추가하기
def reg_loss(self):
return self.l1 * np.sum(np.abs(self.w)) + self.l2 / 2 * np.sum(self.w**2)
4. 검증 세트의 손실을 계산하는 update_val_loss() 메서드에서 reg_loss()를 호출하도록 수정한다.
def update_val_loss(self, x_val, y_val):
if x_val is None:
return
val_loss = 0
for i in range(len(x_val)):
z = self.forpass(x_val[i]) # 정방향 계산
a = self.activation(z) # 활성화 함수 적용
a = np.clip(a, 1e-10, 1-1e-10)
val_loss += -(y_val[i]*np.log(a)+(1-y_val[i])*np.log(1-a))
self.val_losses.append(val_loss/len(y_val) + self.reg_loss())
5. cancer 데이터 세트에 L1 규제 적용하기
규제 강도는 0.0001, 0.001, 0.01 이 세가지로 선택한 후 for문을 사용하여 각각 다른 강도의 하이퍼파라미터로 모델을 만들고 학습 곡선과 가중치를 그래프로 나타내면 다음과 같다.
l1_list = [0.0001, 0.001, 0.01]
for l1 in l1_list:
lyr = SingleLayer(l1=l1)
lyr.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val)
plt.plot(lyr.losses)
plt.plot(lyr.val_losses)
plt.title('Learning Curve (l1={})'.format(l1))
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.ylim(0, 0.3)
plt.show()
plt.plot(lyr.w, 'bo')
plt.title('Weight (l1={})'.format(l1))
plt.ylabel('value')
plt.xlabel('weight')
plt.ylim(-4, 4)
plt.show()맷플롯립의 title() 함수로 제목을 넣고 ylim()함수로 y축의 범위를 제한했다. 왼쪽은 학습 곡선 그래프이고, 오른쪽은 가중치에 대한 그래프이다.


▶ 학습 곡선 그래프를 보면 규제가 더 커질수록 훈련 세트의 손실과 검증 세트의 손실이 모두 높아지는 것을 확인할 수 있다.
즉, 과소적합 현상이 나타난다. 가중치 그래프를 보면 규제 강도 l1값이 커질수록 가중치의 값이 0에 가까워지는 것을 볼 수 있다.
적절한 l1 하이퍼파라미터 값은 0.001정도인 것 같다. 이 값을 사용하여 모델의 성능을 확인해 보면 다음과 같다.

하지만 결과를 보면 규제를 적용하지 않고 검증 세트로 성능을 평가했을 때의 값과 동일하다. 즉, 규제의 효과가 크게 나타나지 않았다.
6. cancer 데이터 세트에 L2 규제 적용하기
l2_list = [0.0001, 0.001, 0.01]
for l2 in l2_list:
lyr = SingleLayer(l2=l2)
lyr.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val)
plt.plot(lyr.losses)
plt.plot(lyr.val_losses)
plt.title('Learning Curve (l2={})'.format(l2))
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.ylim(0, 0.3)
plt.show()
plt.plot(lyr.w, 'bo')
plt.title('Weight (l2={})'.format(l2))
plt.ylabel('value')
plt.xlabel('weight')
plt.ylim(-4, 4)
plt.show()
▶ L2규제도 L1규제와 비슷한 양상을 보이지만 마지막 학습 곡선 그래프를 보면 L2 규제는 규제 강도가 강해져도 L1 규제만큼 과소적합이 심해지지는 않는다. 갖우치 그래프를 보아도 가중치가 0에 너무 가가깝게 줄어들지 않는다는 것도 알 수 있다. 성능은 다음과 같다.

결과를 보니 사실상 cancer 데이터 세트의 샘플 개수가 아주 적어서 L1 규제를 적용한 모델과 L2 규제를 적용한 모델의 성능에는 큰 차이가 없었다.
하지만 차이점은 L1규제를 사용했을 때보다 에포크가 크게 늘어났다는 점이다. 가중치를 강하게 제한했기 때문에 검증 세트의 손실값을 일정한 수준으로 유지하면서 알고리즘이 전역 최솟값을 찾는 과정을 오래 반복할 수 있었던 것이다.
7. SGDClassifier에서 규제 사용하기
사이킷런의 SGDCLassifier클래스도 L1 규제, L2 규제를 지원한다. penalty 매개변수에 l1이나 l2를 매개변수 값으로 전달하고 alpha 매개변수에 규제의 강도를 지정하면 된다.

전체 데이터 세트의 샘플 수가 적을 때 유용하게 사용할 수 있는 또 다른 검증 방법인 교차 검증도 살펴보자
05-4. 교차 검증을 알아보고 사이킷런으로 수행해보기
교차 검증의 원리
교차 검증은 훈련 세트를 작은 덩어리로 나누어 다음과 같이 진행하는데 이때 훈련 세트를 나눈 작은 덩어리를 '폴드'라고 부른다.
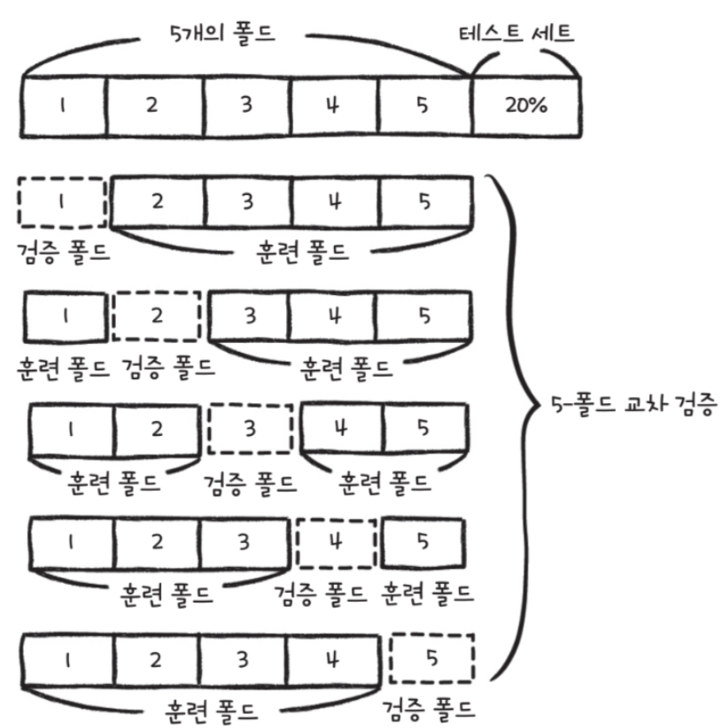
| 교차 검증 과정 - 훈련 세트를 k개의 fold로 나눈다. - 첫 번째 폴드를 검증 세트로 사용하고 나머지 폴드(k-1)개를 훈련 세트로 사용한다. - 모델을 훈련한 다음에 검증 세트로 평가한다. - 차례대로 다음 폴드를 검증 세트로 사용하여 반복한다. - k개의 검증 세트로 k번 성능을 평가한 후 계산된 성능의 평균을 내어 최종 성능을 계산한다. |
K-폴드 교차 검증 구현
1. 훈련 세트 사용하기
기존에는 전체 데이터 세트를 8:2비율로 나누어 훈련 세트와 테스트 세트를 얻고 다시 훈련 세트를 8:2비율로 나누어 훈련 세트와 검증 세트를 얻었다. 즉, 훈련, 검증, 테스트 세트를 완전히 나누었지만 k-폴드 교차 검증은 검증 세트가 훈련 세트에 포함된다.
각 폴드의 검증 점수를 저장하기 위한 validation_scores 리스트를 정의하고 리스트의 값을 평균하여 최종 검증 점수를 계산한다.
validation_scores = []
2. k-폴드 교차 검증 구현하기
아래 코드에서 신경 써서 봐야 할 부분은 훈련 데이터의 표준화 전처리를 폴드를 나누 후에 수행한다는 점이다.
k = 10 # 10번 반복
bins = len(x_train_all) // k # 한 폴드에 들어갈 샘플의 개수를 bins변수에 저장
for i in range(k):
# start와 end는 각각 검증 폴드 샘플의 시작과 끝 인덱스이고, 나머지 부분이 훈련 폴드 샘플의 인덱스
start = i*bins
end = (i+1)*bins
val_fold = x_train_all[start:end]
val_target = y_train_all[start:end]
# train_index에 list()함수를 이용하여 훈련 폴드 샘플의 인덱스를 모아둔다.
# 이렇게 만든 훈련 폴드 샘플의 인덱스로 train_fold와 train_target을 만든다.
train_index = list(range(0, start))+list(range(end, len(x_train_all)))
train_fold = x_train_all[train_index] # x_train_all[[1,2,3,....start,end....]]
train_target = y_train_all[train_index] # y_train_all[[1,2,3,....start,end....]]
train_mean = np.mean(train_fold, axis=0)
train_std = np.std(train_fold, axis=0)
train_fold_scaled = (train_fold - train_mean) / train_std
val_fold_scaled = (val_fold - train_mean) / train_std
lyr = SingleLayer(l2=0.01) # L2 규제를 사용하며 강도는 0.01로 한다.
lyr.fit(train_fold_scaled, train_target, epochs=50)
score = lyr.score(val_fold_scaled, val_target)
validation_scores.append(score)
# 반복문을 진행하며 10개의 검증 폴드로 측정한 성능 점수는 validation_scores 리스트에 저장된다.
print(np.mean(validation_scores))
# 0.9711111111111113
사이킷런으로 교차 검증 하기
1. cross_validate() 함수로 교차 검증 점수 계산하기
함수의 매개변수 값으로 교차 검증을 하고 싶은 모델의 객체와 훈련 데이터, 타깃 데이터를 전달하고 cv 매개변수에 교차 검증을 수행할 폴드 수를 지정하면 된다.
# 사이킷런의 model_selection 모듈에는 교차 검증을 위한 cross_validate()함수가 있다.
from sklearn.model_selection import cross_validate
sgd = SGDClassifier(loss='log', penalty='l2', alpha=0.001, random_state=42)
scores = cross_validate(sgd, x_train_all, y_train_all, cv=10)
print(np.mean(scores['test_score']))
# 0.850096618357488cross_validate()함수는 파이썬 딕셔너리를 반환한다. 검증 점수는 scores['test score']에 저장되어 있다. 교차 검증의 평균 점수는 약 85%로 낮은 편이다. 낮은 이유는 표준화 전처리를 수행하지 않았기 때문이다.
전처리 단계 포함해 교차 검증 수행하기
Pipeline 클래스 사용해 교차 검증 수행하기
- 사이킷런은 검증 폴드가 전처리 단계에서 누설되지 않도록 전처리 단계와 모델 클래스를 하나로 연결해주는 Pipeline클래스를 제공한다.
- 먼저 표준화 전처리 단계(평균, 표준 편차를 계산)와 SGDClassifier클래스 객체를 Pipeline클래스로 감싸 cross_validate()함수에 전달한다.
- 그러면 cross_validate()함수는 훈련 세트를 훈련 폴드와 검증 폴드로 나누기만 하고 전처리 단계와 SGDClassifier클래스 객체의 호출은 Pipeline 클래스 객체에서 이루어진다. 이렇게 되면 검증 폴드가 전처리 단계에서 누설되지 않게 된다.
- make_pipeline()함수에 전처리 단계와 모델 객체를 전달하면 파이프라인 객체를 만들 수 있다.
▶ 사이킷런에서 표준화 전처리를 수행하는 StandardScaler클래스의 객체와 SGDClassifier클래스의 객체를 make_pipeline()함수에 전달하여 파이프라인 객체를 만들어 본 후 다시 교차 검증 점수를 출력해보자
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
pipe = make_pipeline(StandardScaler(), sgd)
scores = cross_validate(pipe, x_train_all, y_train_all, cv=10, return_train_score=True)
print(np.mean(scores['test_score']))
# 0.9694202898550724
print(np.mean(scores['train_score']))
# 0.9875478561631581평균 검증 점수가 높아진 것을 확인할 수 있다. 추가로 cross_validate()함수에 return_train_score 매개변수를 True로 설저하면 훈련 폴드의 점수도 얻을 수 있다.
< 참고 자료 >
Do it! 딥러닝 입문 - 박해선 지음
'딥러닝,인공지능 > Do it! 딥러닝입문' 카테고리의 다른 글
| 06. 2개의 층을 연결하자(다층 신경망) - 배치경사하강법 (0) | 2021.05.21 |
|---|---|
| 05. 훈련노하우 - 검증 세트와 전처리 과정, 과대/과소 적합 (0) | 2021.05.05 |
| 04. 데이터 세트 분류, 로지스틱 회귀 (0) | 2021.05.05 |
| 04. 분류하는 뉴런 만들기 - 이진 분류(3) (0) | 2021.04.04 |
| 04. 분류하는 뉴런 만들기 - 이진 분류(1)(2) (0) | 2021.04.04 |




